Module 1: Basic Notions of Computing and Programming#
In this Module we discuss some basic notions of computing and what is a programming language. We then experiment with a simple programmable computer architecture called BlinkenBits.
Some Basic Notions of Computing#
This section explains the meaning of “programming a computer” through A Very Brief History of Computing and Programming. You do not need to remember the details of the historical evolution of computing — but seeing how problems and challenges were addressed in the past may help better understand why modern computers are designed and programmed in a certain way.
Then, we will briefly discuss the interfaces for interaction between humans and computers, how how data and programs are stored.
A Very Brief History of Computing and Programming#
A key element that drives human progress is the ability to define and perform computations, i.e. take one or more inputs and produce one or more outputs or results. In order to turn inputs into results, it is necessary to apply an algorithm, i.e. follow a sequence of rigorous steps.
Example 1 (Computing the area of a room)
If we want to compute the area of a room, we can apply the following algorithm (for brevity, some cases are omitted with “…”).
We take the room measures as input (number of sides, their length, the angles at the corners), and:
We determine (i.e. compute) what is the shape of the room. To do this, we follow an algorithm: we take the room measures as input, and check:
If the room has 4 sides with 90° angles at each corner, then the result is that the shape is a rectangle;
If the room has 3 sides, then the result is that the shape is a triangle;
…
Then, using the room measures and shape as input, we compute the room area. We follow this algorithm:
If the room shape is a rectangle, we take the measures of two adjacent sides (the inputs), we compute their multiplication, and the result is the area.
To compute the multiplication, we take the multiplication arguments (the inputs), we follow the steps of the long multiplication algorithm, and we produce the desired result.
If the room shape is a triangle, …
…
As you can notice from Example 1, in order to compute a result we may need to perform intermediate computations — e.g. we must first determine the shape of a room, and then we can decide which algorithm is appropriate for computing its area.
Early Computers: People and Devices#
Historically, the term computer has been used to indicate a person that performs computations as a job: for instance, in the 15th and 16th century, astronomers often called themselves “computers” (because they spent most of their time calculating the orbits of planets), and hired “computers” as assistants to help them.

Fig. 1 British royal astronomer John Flamsteed (at the telescope on the left) and his paid assistant (at the table, probably doing some computing). Etching from 1677-78. (© The Trustees of the British Museum; CC BY-NC-SA 4.0; Museum number: 1865,0610.952.)#
The term “computer” has been used with the meaning “human computer until the 1960s: for instance, between the 1940s and 1960s, NASA (and its precursor NACA) used human computers to calculate the trajectories of rockets, satellites, and spaceships, and plan the early space missions.

Fig. 2 The team of computers working on the calculations of the orbit of the Explorer 1 satellite. Photo from the 1950s. (Image from the NASA archives; public domain.)#
However, performing computations by hand can be very time-consuming and error-prone. Therefore, many devices have been developed throughout history to help (and later replace) human computers. Early computing devices were mechanical, and later electronic. Their main drawback was that they were fixed-function, i.e. they were designed and built to perform some specific computations on the given inputs (e.g. some specific sequences of additions, multiplications, division, …) and produce a result. Extending those devices to perform new types of computation was very hard: the designers needed to add more physical components (e.g. more mechanical gears, more electric relays, more vacuum tubes…) which made the devices more complex, and therefore more expensive — and often more fragile and less reliable.

Fig. 3 A difference engine, designed in the 1820s. The machine implements a fixed computation using mechanical gears. Its input values are set by configuring the gears and wheels in the columns; when the crank handle (on the bottom left corner) is operated, the machine computes its result. (Image by Canticle at English Wikipedia; CC BY-SA 3.0; https://commons.wikimedia.org/w/index.php?curid=10532728.)#

Fig. 4 A McDonnell F-101 Voodoo supersonic fighter jet. Introduced in 1957, this plane had an on-board electrical-mechanical computer (see Fig. 5 below), used e.g. to perform the sophisticated computations required to estimate the air speed. (Image by RuthAS at English Wikipedia; CC BY 3.0; https://commons.wikimedia.org/w/index.php?curid=26995763.)#

Fig. 5 The Bendix Central Air Data Computer (CADC). Developed in the 1950s, this computer was mounted on various warplanes — including the McDonnell F-101 Voodoo fighter jet (Fig. 4). The computer received air pressure and temperature inputs from tubes and sensors mounted on the plane, and it performed various fixed computations (e.g., air speed and air density); the outputs of such computations were shown to the pilot on the cockpit dials. The computations were performed via a complicated mix of electrical and mechanical components. If you are curious, you can find more details and see this computer in action on this blog post. (Image by KenShirriff at English Wikipedia; CC BY-SA 4.0; https://commons.wikimedia.org/w/index.php?curid=124396068.)#
Programmable Computing Machines#
Later computing devices were designed as programmable machines: the machine offered a set of built-in operations (e.g. additions, multiplications, divisions, …), and the users could configure the machine to perform such operations in a certain order, or under certain conditions, using the output of an operation as an input for the next operation. This way, the users were able to set up the machine to perform new algorithms, resulting in new kinds of computations. These machines had some form of memory or storage, i.e. some way to store the inputs and the results of the ongoing computation (using e.g. the positions of mechanical gears, or light dots in cathode-ray tubes) and retrieve them later for further computations.
To program a computing machine of this kind, the user needed to physically alter its setup to control the flow of computations: e.g. the users had to manually connect or disconnect electric wires, turn switches on or off, or punch holes into a card to mechanically activate/deactivate some switches. In other words: “programming a computer” meant “configuring the hardware of the computer to make it execute a desired algorithm.”

Fig. 6 A data center with an IBM 604 calculator (in the middle). Introduced in 1948, this electric computer was programmed with a plugboard like the one in Fig. 7. (Image by Norsk Teknisk Museum; CC BY-SA 4.0; https://digitaltmuseum.org/011015239225/6-3-ibm-datasenter.)#

Fig. 7 Plugboard of an IBM 604 calculator: by changing the wiring, it was possible to select different sequences of computations. (Image by National Museum of American History; only usable for personal, educational, and other non-commercial uses; https://americanhistory.si.edu/collections/search/object/nmah_334753)#
Stored-Program Computers and the Von Neumann Architecture#
Compared to human computers, the early programmable machines discussed above had a fundamental limitation: they could only be programmed via physical (hardware) modifications. Instead, a human computer can be “programmed” by loading a new algorithm in memory — i.e. a human computer can read and remember the steps of an algorithm. Consequently, a human computer can apply an algorithm by taking some inputs, recalling the desired algorithm steps from memory, executing such steps, and producing a result.
In a similar fashion, the next phase in the evolution of computing devices were stored-program computers, i.e. machines that could load in their memory the steps of the algorithms that they execute.
This means that a user could program this kind of machine by loading a desired sequence of machine instructions (a.k.a. machine code) in its memory, without physically modifying the machine hardware. Each machine instruction specifies an operation that the machine’s Central Processing Unit (CPU) can execute, e.g.:
receive an input from an external device and save it in a memory location;
read the content of a memory location and send it to an output device;
read the values stored in two memory locations, compute their sum, and store the result in another memory location;
check if the value stored in a certain memory location is equal to 0;
execute the machine instruction stored in a certain memory location;
…
A sequence of such machine instructions is a program, and corresponds to the steps of a desired algorithm.

Fig. 8 A replica of the Manchester Baby, the first fully-electronic stored-program computer: it ran its first program on 21 June 1948. (Photo by Parrot of Doom, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=8318196.)#
The idea of stored-program computer was introduced in the late 1940s by John von Neumann — and indeed, the von Neumann architecture is the foundation of what we call a “computer” today: a stored-program electronic computing machine. From now on, we will use the term “computer” with this meaning; and from this point in history, “programming a computer” means “write the software (i.e. the program) that the computer can load in memory and execute.”
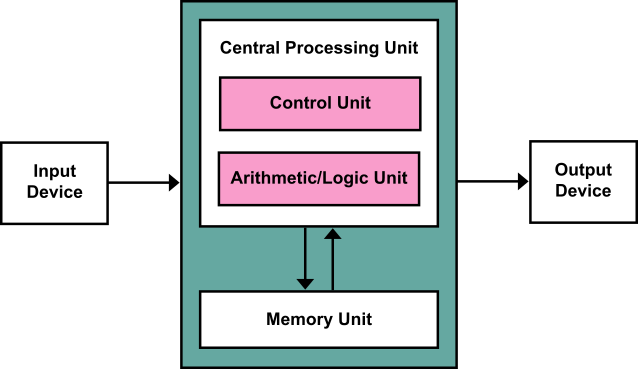
Fig. 9 A diagram of the von Neumann architecture. The Central Processing Unit (CPU) can load machine instructions from the memory and execute them (via its Control Unit); such instructions allow the CPU to perform computations (via the Arithmetic/Logic Unit) and read or write the data stored in the memory. The machine instructions can also perform input and output of data from/to external devices. (Diagram by Kapooht; CC BY-SA 3.0; https://commons.wikimedia.org/w/index.php?curid=25789639.)#
Modern Computers#
Stored-program computers are very flexible. Since their first prototypes (1950s) their adoption has exploded, leading to new application areas, and new demands requiring improved performance — e.g. faster computation speeds, larger memory sizes, smaller dimensions, lower power consumption. Modern computers range from very small (e.g. smart watches and cellphones) to very large (e.g. high-performance supercomputers used for scientific simulations). All of these different computers, at their core, are based on some variation of the von Neumann architecture: they all work by loading a sequence of machine instructions into their memory, and then executing such instructions — which may input and output data from/to external devices, and read and write data from/to the computer memory.
During the evolution of computers, many different ideas, approaches, and design variants have been proposed: for example, there exist several different types of Central Processing Units (CPUs) that execute different machine instructions — which means that e.g. a computer with an Intel or AMD x86 CPU cannot execute the machine instructions supported by an ARM CPU, and vice versa.
Luckily, several aspects have been standardised across different computer brands and designs. For example:
Data and machine instructions are stored in the computer memory as numbers in binary representation. A single “binary digit” can have value 0 or 1, and is called bit; a group of 8 bits is called byte. Storing larger numbers requires more bits and bytes, and thus, more memory: for example, the decimal number 3147483647 is represented in binary as 10111011100110101100100111111111, hence it requires 32 bits (i.e. 4 bytes) of computer memory.
Text is also stored in the computer memory using binary numbers — with each text character represented by a different number: for example, the character
Ais represented in memory by the binary number 01000001 (corresponding to the decimal number 65). The modern rules for representing (encoding) text characters as numbers are specified in The Unicode Standard.
Interaction Between a Human and a Computer#
Early stored-program computers were not easy to use: as you can see in Fig. 8, the users were often expected to flip switches and press buttons on a control panel to modify the contents of the computer’s memory, one bit at a time, or read the memory contents by looking at the computer’s blinkenlights.
To simplify and speed up their usage, computers were later equipped with programs that could send and receive data from a teleprinter (a.k.a. teletypewriter or teletype): the users would type commands on the teletype; the program running on the computer would receive such commands, and then send its output back to the teleprinter, which would print that output on a roll of paper. Teleprinters connected to computers were called terminals or consoles, and they offered a so-called command-line interface (CLI) for using the computer.

Fig. 10 An IBM System/360 computer, with an operator using its command-line interface on a teleprinter terminal. Photo from the 1960s. (From the IBM archives; https://www.ibm.com/ibm/history/ibm100/us/en/icons/system360/impacts/.)#
Teleprinters were noisy and cumbersome to use, so they were later superseded by Video Display Units (VDU)s consisting of a monitor (replacing the roll of paper of a teletype) and a keyboard (similar to a typewriter, but much quieter!). Users were now able to operate the computer by typing commands on a keyboard and seeing the computer’s feedback on a video display.

Fig. 11 A DEC VT100 video terminal (monitor and keyboard on the left) connected to a DEC PDP-11/70 computer (on the right). Both the computer and the terminal were produced around the late 1970s. (Photo by Matthew Ratzloff; CC BY-NC-ND 2.0; https://www.flickr.com/photos/mratzloff/9169358863.)#
Later developments made computers even easier to use — especially with the introduction of graphical user interfaces (GUI), usable by clicking on visual elements.
However, the old-school text-based interfaces are still in use today: all major computer operating systems (including Windows, macOS, and Linux) provide some command-line interface resembling a terminal from the 1970s, allowing users to issue commands (e.g. load a program from a solid-state drive into memory and execute it) and see the resulting output. We will use such command-line interfaces during this course, because they allows us (as programmers) to better understand what is happening “under the hood” of the user-friendly graphical interface.
Fig. 12 Screenshot of Windows 10 with one of its command-line interfaces.#
Storage of Data and Programs#
Another crucial element in the history of computing is the development of storage for data (e.g. numbers, text, …) and programs (i.e. the machine instructions that are executed by the CPU). In the von Neumann architecture (and thus, in modern computers) the only storage that the CPU can access directly is the Random Access Memory (RAM), that is also called the primary storage. The RAM is very fast but limited in size, especially because its cost (i.e. its price per byte) is very high; moreover, its contents are lost when the computer is powered off.
For this reason, computers include secondary storage to hold programs and data in a more permanent way. Old computers used e.g. rolls of magnetic tape (visible in Fig. 10) or floppy disks as secondary storage, while modern computers often include e.g. a solid-state drive (SSD). The secondary storage is slower than RAM, but it is also much cheaper and thus larger in size: for example, a typical modern laptop computer may only hold 16 Gigabytes of data and programs in its RAM, while it may hold hundreds or thousands of Gigabytes of data and programs in its SSD. Moreover, the data and programs saved in the secondary storage are not lost when the computer is powered off. A drawback of secondary storage is that the computer’s CPU cannot typically access its contents directly. This means that:
The CPU cannot directly execute a program stored e.g. on an SSD: the program must be first loaded into the computer’s RAM, and then executed.
A program cannot make the CPU compute a result by directly using data stored in an SSD: the program must first load the relevant data into the computer RAM (by using e.g. some CPU instructions for input/output); then, the program can direct the CPU to read the loaded data to compute the desired result.
What is a Programming Language?#
We have seen that a computer works by executing a sequence of machine instructions stored in its memory. But what do these machine instructions look like?
Recalling the opening example, suppose that we want to compute the area of a rectangle having width 3 and height 7, and then show the result on the computer screen. To do that on a computer with a RISC-V CPU, we could load the following sequence of machine instructions (one per line) in the computer’s memory, and execute them:
00000000001000000000010000110011
00000000001000000000001010010011
00000000011100000000001100010011
00000000010100000000001110110011
00000000011000000000010010110011
00000010100100111000001110110011
00000000011100000000010010110011
11111111100000010000000100010011
00000001000100010010000000100011
00000000101000010010001000100011
00000000100100000000010100110011
00000000000100000000100010010011
00000000000000000000000001110011
The program above is not very readable — and yet, this is how early programmers wrote their programs in the first stored-program computers!
To make their lives a bit easier, those early programmers wrote the first assemblers, i.e. programs that translate sequences of assembly instructions (that are easier to read and write for humans) into machine instructions. The translation process is called compilation. For instance, an assembler can translate the following sequence of assembly instructions into the machine instructions above:
mv fp, sp
li t0, 3
li t1, 7
mv t2, t0
mv s1, t1
mul t2, t2, s1
mv s1, t2
addi sp, sp, -8
sw a7, 0(sp)
sw a0, 4(sp)
mv a0, s1
li a7, 1
ecall
Assembly instructions are a rudimentary form of programming language, i.e. a notation and a series of rules for writing programs that can be translated into machine instructions and executed by the CPU of a computer.
Programs written in assembly are still not very readable for humans, because assembly is a low-level language — i.e. each assembly instruction closely corresponds to a machine instruction. For this reason, many high-level programming languages have been developed throughout the history of computing (and new ones are being developed nowadays): such languages allow us to write programs with a notation that resembles plain English and mathematical formulas. Therefore, programs written in high-level languages are much easier to write, read, and understand for humans, compared to programs written in assembly.
For example, the Java programming language allows us to write a program that looks (roughly) like the following snippet of code:
var width = 3;
var height = 7;
var area = width * height;
print(area);
By reading this Java code, one can quite easily guess what it is doing (unlike the assembly and machine instructions above). The main goal of this course we will learn how to program a computer using the Java programming language.
Experimenting with BlinkenBits#
As mentioned above, high-level languages like Java are typically easier to read and write than assembly, because they “hide” many details of the underlying computer. This is generally desirable, but there is also a drawback: Java comes with many concepts and tools that can be hard to grasp, especially if one does not know how a computer works, and if one does not have previous programming experience.
For this reason, before delving into Java, and in order to better grasp how a computer works “under the hood” and how it can be programmed, we experiment with a very limited and teaching-oriented computer called BlinkenBits. BlinkenBits is not real hardware, but you can use it via a web-based emulator:
https://courses.compute.dtu.dk/02312/e24/BlinkenBits
An Overview of BlinkenBits#
BlinkenBits is based on the Von Neumann architecture, i.e., it has a memory that can contain both data and machine instructions. More in detail:
BlinkenBits has 64 memory locations, each one having an address between 0 and 63. Each memory location holds a value between 0 and 4095 (because each memory location contains 12 bits). The value held by each memory location can be read or written by dedicated machine instructions (see below).
The 8 memory locations with addresses in the range 56–63 are connected to a 8-character display: e.g., if the memory location at address 56 contains the value 5, the first display element shows the number 5. (For more details, see The BlinkenBits Display.)
BlinkenBits also has 4 registers called
r0,r1,r2, andr3. Each register can be used to hold a value; in the case of BlinkenBits, such a value must be between 0 and 4095 (this is because each register contains 12 bits). The value held by each register can be used by dedicated machine instructions to perform computations, e.g., additions and subtractions (see below).BlinkenBits recognises 11 different machine instructions, which can perform tasks such as: write a value into a register, add or subtract the contents of two registers, store the value held in a register into a memory location — or vice versa, load the value held in a memory location into a register. (The BlinkenBits instructions are illustrated in The BlinkenBits Machine Instructions and The BlinkenBits Assembly Language.)
BlinkenBits reads and executes machine instructions that are contained in its memory locations; the program counter (PC) is a special register that holds the memory address of the next instruction to be executed.
When BlinkenBits powers up (or after it resets), every register and memory location holds the value 0, and the program counter (PC) also contains 0: therefore, BlinkenBits is ready to execute whatever instruction is held in the memory location with address 0.
Important
From the description above, the memory locations may appear similar to the
registers r0…r3: indeed, they both hold 12-bit values. As we will see
shortly, the main difference
between the two is that the BlinkenBits machine instructions can only perform
computations (additions, subtractions…) using values held in registers;
consequently, a value held in a memory location can only be used in a
computation after the value has been loaded into a register.
The BlinkenBits Display#
The BlinkenBits emulator has a 8-element display, where each element shows a symbol that corresponds to the content of a memory location with address in the range 56-63. Table 1 below summarises how the values stored at memory addresses 56–63 are visualised on the BlinkenBits display.
Value(s) |
Displayed as… |
|---|---|
0…9 |
Digits |
10…35 |
Lowercase letters |
36…61 |
Uppercase letters |
62 |
Underscore |
63 |
Dot |
64 |
Comma |
65 |
Semicolon |
66 |
Exclamation mark |
67 |
Question mark |
68 |
Plus sign |
69 |
Minus sign |
70 |
Asterisk |
71 |
Slash |
72…4095 |
|
Exercise 1 (Experimenting with BlinkenBits (1))
Try visualising the symbols listed in Table 1 at different positions on the BlinkenBits display. For instance, try writing the following values:
value 43 at the memory location with address 56
value 14 at the memory location with address 57
value 19 at the memory location with address 58
value 66 at the memory location with address 59
value 62 at the memory locations with addresses 60…63
The BlinkenBits Machine Instructions#
As mentioned above, BlinkenBits recognises 11 different machine instructions. Each instruction is codified as a value in the range 0…4095.
Example 2 (BlinkenBits machine instructions)
The value 0 represents the “halt” instruction: when BlinkenBits executes it, it simply does nothing and stops. (See Exercise 2 below.)
The value 3076 represents a “register copy” instruction. More specifically: when BlinkenBits executes that instruction, it copies the content of register
r0into registerr1. (See Exercise 3 below.)The value 289 represents an “add” instruction. More specifically: when BlinkenBits executes that instruction, it read the contents of registers
r0andr1, computes their addition, and writes the result into registerr2. (See Exercise 4 below.)
Important
Many values do not correspond to any machine instruction: for instance, BlinkenBits produces an error if it tries to “execute” the value 42. (See Exercise 5 below.)
To program BlinkenBits, a programmer needs to fill its memory locations with
values that represent the intended machine instructions. Then, the programmer
can press the “run” button (⏵) to execute such instructions. The
next instruction to be executed is always the one contained in the memory
location whose address is in the BlinkenBits’ program counter (PC); after
an instruction is executed, the PC is updated with the address of the next
instruction to be executed. (The only exception is the “halt” instruction, which
stops the execution without updating the PC.)
Exercise 2 (Experimenting with BlinkenBits (2))
Try resetting BlinkenBits (button ⏻): the computer status will become
“Ready” to execute the instruction at the memory location with address 0 —
because the program counter (PC) points to that memory address.
Now, press either the button 1⏵ (execute next instruction) or ⏵ (run):
BlinkenBits will execute the instruction pointed by the PC, i.e., at the memory
location with address 0. That memory location contains the value 0, which (as
mentioned in Example 2 above) represents
machine instruction “halt.” Consequently, BlinkenBits will change its status to
“Halted.”
Exercise 3 (Experimenting with BlinkenBits (3))
Try resetting BlinkenBits (button ⏻): the computer status will become
“Ready” to execute the instruction at the memory location with address 0 —
because the program counter (PC) points to that memory address.
Now, follow these steps:
Write the value 3076 in the memory location at address 0.
As mentioned in Example 2, this value represents a “register copy” instruction from register
r0to registerr1.
Write a value you like in the register
r0.Press the button
1⏵(execute the next instruction).BlinkenBits will execute the instruction pointed by the PC (i.e., contained in the memory location with address 0). That instruction makes BlinkenBits copy the content of register
r0into registerr1. (Note that the web-based emulator highlights registers in green when they are read, and in light red when they are written).Also observe that BlinkenBits has incremented the value of PC from 0 to 1: therefore, the next instruction to be executed is contained in the memory location with address 1.
Now, press the button
1⏵again.BlinkenBits will execute the instruction pointed by the PC (i.e., contained in the memory location with address 1). That memory location contains the value 0, which corresponds to the “halt” instruction: therefore, BlinkenBits will now halt, similarly to Exercise 2 above.
Exercise 4 (Experimenting with BlinkenBits (4))
Try resetting BlinkenBits (button ⏻): the computer status will become
“Ready” to execute the instruction at the memory location with address 0 —
because the program counter (PC) points to that memory address.
Now, follow these steps:
Write the value 289 in the memory location at address 0.
As mentioned in Example 2, this value represents a “register add” instruction that adds the values in
r0andr1and writes the result inr2.
Write two values you like in the registers
r0andr1.Press the button
1⏵(execute the next instruction).BlinkenBits will execute the instruction pointed by the PC (i.e., contained in the memory location with address 0). That instruction makes BlinkenBits read the contents of the registers
r0andr1, add them, and write the result into registerr2. Note that:the web-based emulator highlights registers in green when they are read, and in light red when they are written;
if the addition of the two values in the registers
r0andr1exceeds the maximum value 4095, the computation will “wrap around” and only produce the part of the result that exceeds 4096. For instance, if registersr0andr1contain the values 4000 and 195, their addition will produce the result 99 in registerr2. This is similar to a car odometer that can only count up to 999,999 km, and restarts from 000,000 once it reaches 1,000,000 km.
Also observe that BlinkenBits has incremented the value of PC from 0 to 1: therefore, the next instruction to be executed is contained in the memory location with address 1.
Now, press the button
1⏵again.BlinkenBits will execute the instruction pointed by the PC (i.e., contained in the memory location with address 1) and will halt, similarly to Exercise 2 above.
Exercise 5 (Experimenting with BlinkenBits (5))
Try resetting BlinkenBits (button ⏻): the computer status will become
“Ready” to execute the instruction at the memory location with address 0 —
because the program counter (PC) points to that memory address.
Now, follow these steps:
Write the value 42 in the memory location at address 0.
As mentioned in Example 2, this value does not represent a valid BlinkenBits machine instruction.
Press the button
1⏵(execute the next instruction).BlinkenBits will try to execute the instruction pointed by the PC, i.e., contained in the memory location with address 0. However, the value 42 contained in that memory location does not represent a valid machine instruction — and consequently, BlinkenBits will change its status to “Error.”
The BlinkenBits Assembly Language#
Programming BlinkenBits by writing machine instructions as numeric values into its memory is possible (this is what early computer programmers did!), but quite cumbersome. To make programming a bit faster and intuitive, each machine instruction has a more human-friendly representation in BlinkenBits assembly, which is a rudimentary programming language.
Example 3 (BlinkenBits assembly instructions)
Let us consider again the machine instructions discussed in Example 2, and let us see their assembly representation:
The value 0 represents the “halt” instruction, and is written in BlinkenBits assembly as halt.
The value 3076 represents a “register copy” instruction that is written in BlinkenBits assembly as r1 <- r0 (i.e., copy the content of register
r0into registerr1).The value 289 represents an “add” instruction that is written in BlinkenBits assembly as r2 <- r0 + r1 (i.e., add the values contained in registers
r0andr1, write the result into registerr2).
Important
Like all computers, BlinkenBits does not directly execute assembly instructions: as mentioned above, assembly instructions are just a human-oriented representation of the actual machine instructions. In order to be executed, assembly instructions must be first translated into the corresponding machine instructions — and such machine instructions can be then executed by BlinkenBits.
For convenience, the BlinkenBits web-based emulator translates assembly into machine instructions (and vice versa) on-the-fly, so you can immediately see how they correspond to each other.
BlinkenBits supports 11 assembly instructions, which are grouped in the 3 categories below.
Register computation instructions (Table 2): these instructions perform computations that read input values contained in zero, one, or two registers, and produce a result value which is written into a destination register.
Register-memory transfer instructions (Table 3): these instructions allow for transferring values from registers to memory, and vice versa.
Execution control instructions (Table 4): these instructions allow for controlling which instruction BlinkenBits will execute next. More specifically, these instructions can be used to jump to another instruction (possibly depending on a condition), or halt the execution.
Furthermore, one can write the assembly “non-instruction” data \(n\) to describe that a memory location contains the value \(n\). The value \(n\) may not correspond to any machine instruction. (NOTE: \(n\) must be in the range 0…4095).
Assembly instruction |
Description |
|---|---|
r\(d\) <- \(n\) |
Write the value \(n\) into register r\(d\). NOTE: \(n\) must be in the range 0…63. |
r\(d\) <- r\(s\) |
Copy the content of register r\(d\) into register r\(s\). |
r\(d\) <- r\(s_1\) + r\(s_2\) |
Add the values contained in registers r\(s_1\) and r\(s_2\), and then write the result into register r\(d\). |
r\(d\) <- r\(s_1\) - r\(s_2\) |
Subtract the value contained in register r\(s_2\) from the value in register r\(s_1\), and then write the result into register r\(d\). |
r\(d\) <- r\(s_1\) < r\(s_2\) |
If the value contained in register r\(s_1\) is smaller than the value in register r\(s_2\), write 1 into r\(d\); otherwise, write 0 into r\(d\). |
r\(d\) <- r\(s_1\) == r\(s_2\) |
If the value contained in register r\(s_1\) is equal to the value in register r\(s_2\), write 1 into r\(d\); otherwise, write 0 into r\(d\). |
Assembly instruction |
Description |
|---|---|
r\(d\) <- memory@r\(s\) |
Load the value at the memory location whose address is contained in register r\(s\), and write that value into register r\(d\). |
memory@r\(s_1\) <- r\(s_2\) |
Store the content of register r\(s_2\) into the memory location whose address is contained in register r\(s_1\). |
Assembly instruction |
Description |
|---|---|
jump \(n\) |
Write the value \(n\) in the program counter (PC). As a consequence, BlinkenBits will “jump” to the instruction at memory address \(n\), which will be executed next. NOTE: \(n\) must be in the range 0…63. |
if r\(s\) jump \(n\) |
Conditional jump: if the content of register r\(s\) is not 0, write the value \(n\) in the program counter (PC); otherwise, increment the PC by 1, to execute the next instruction as usual. NOTE: \(n\) must be in the range 0…63. |
halt |
Halt the execution. |
The next examples describe how to solve various tasks by writing small programs in BlinkenBits assembly.
Example 4 (Loading a large value into a register (1))
Our goal is to write a BlinkenBits assembly program that puts the value 150 into
register r0.
We may try putting the value 150 directly into r0 by writing the assembly
instruction r0 <- 150 — but if you try, you will get an error. Indeed,
according to Table 2, this instruction is
invalid, because the value must be in the range 0…63 (although a register can
contain values in the range 0…4095). Therefore, we need to find another way to
achieve our objective.
By looking at the other instructions in
Table 2, we can observe that BlinkenBits
provides an addition instruction between values contained in registers.
Therefore, we could solve the task by writing a few values in the range 0…63
into the available registers, and then adding such values, until we obtain the
value 150 in register r0, as required. For example, after resetting
BlinkenBits (button ⏻), you could write the following assembly instructions at
the memory addresses listed in this table, and then execute the instructions
(either step-by-step by clicking the button 1⏵, or in sequence by clicking the
button 1⏵).
Memory address |
Assembly instruction |
Comment |
|---|---|---|
00 |
r1 <- 63 |
Write value 63 into register r1 |
01 |
r2 <- 63 |
Write value 63 into register r2 |
02 |
r3 <- 24 |
Write value 24 into register r3 |
03 |
r0 <- r1 + r2 |
Add values contained in r1 and r2, write result in r0 |
04 |
r0 <- r0 + r3 |
Add values contained in r0 and r3, write result in r0 |
05 |
halt |
End of the program |
Important
To speed up assembly programming in BlinkenBits, you can click on “Edit or upload assembly code…” (top-right corner on the BlinkenBits emulator) and use the pop-up window to directly edit or copy&paste whole assembly programs with multiple instructions and comments (instead of editing one memory location at a time). Each line of the assembly program must have the following format:
memory address
:assembly instruction//comment (optional)
If a memory address is not explicitly listed in the program, it will contain the
halt instruction.
For instance, the following assembly program corresponds to the assembly instructions and comments shown in Example 4. The following program can be copy&pasted directly on the BlinkenBits “Edit or upload assembly…” interface. (Try it!)
00: r1 <- 63 // Write value 63 into register r1
01: r2 <- 63 // Write value 63 into register r2
02: r3 <- 24 // Write value 24 into register r3
03: r0 <- r1 + r2 // Add values contained in r1 and r2, write result in r0
04: r0 <- r0 + r3 // Add values contained in r0 and r3, write result in r0
05: halt // End of the program
From now on, we will use this format when discussing BlinkenBits assembly programs.
Example 5 (Progressively increasing the value contained in a register (1))
Our goal is to write a program that increases the value contained in register
r0 by adding 1 to its current value.
A possible solution is to write a program that performs consecutive increments as follows:
00: r0 <- 0 // Initialize r0 with value 0
01: r1 <- 1 // Initialize r1 with value 1 (to be used for increments)
02: r0 <- r0 + r1 // Increment r0 by 1
03: r0 <- r0 + r1 // Increment r0 by 1
04: r0 <- r0 + r1 // Increment r0 by 1
05: r0 <- r0 + r1 // Increment r0 by 1
06: r0 <- r0 + r1 // Increment r0 by 1
07: r0 <- r0 + r1 // Increment r0 by 1
08: r0 <- r0 + r1 // Increment r0 by 1
09: r0 <- r0 + r1 // Increment r0 by 1
10: r0 <- r0 + r1 // Increment r0 by 1
// ...
You can notice that we are repeating the same instruction r0 <- r0 + r1 over and over again — and such repetitions make the program longer. Moreover, with this approach we cannot increment r0 beyond the value 61, because we will run out of memory locations for writing more instructions!
When we want to repeat one or more instructions, we can use the jump instruction listed in Table 4. For instance, we could try the following assembly program:
00: r0 <- 0 // Initialize r0 with value 0
01: r1 <- 1 // Initialize r1 with value 1 (to be used for increments)
02: r0 <- r0 + r1 // Increment r0 by 1
03: jump 2 // Jump to memory location at address 2
When executed, this program performs the required increments — and it will keep running until BlinkenBits is paused or reset.
Note
If you let the program above run long enough, you will notice that when r0
reaches the maximum value 4095, the next increment will make it “wrap around”
to 0, and the increments will continue from there.
Remark 1 (Sketching algorithms using flowcharts)
When planning how to write a program that solves a certain task, it can be helpful to first sketch a flowchart that describes an algorithm that solves the task. The flowchart breaks down the task into a sequence of steps, represented as boxes. Since our goal is to program BlinkenBits, each box in the flowchart should correspond to an activity that BlinkenBits can perform by executing one (or a few) instructions. For instance, a rough algorithm for the task in Example 5 could be sketched as the following flowchart:
This flowchart does not yet precisely convey which assembly instructions we
could use: in particular, there is no BlinkenBits instruction that can perform
the activity in the rightmost box (“increment r0 by 1”) at once. The only way to
increment r0 is to add to r0 the value contained in another register, e.g.,
r1; therefore, in order to “increment r0 by 1,” we first need to put the
value 1 in r1, and then add the value in r1 to r0 (writing the result in
r0 itself). With these considerations, we can refine the flowchart above, and
we get:
From this refined flowchart we can more directly derive the assembly code
shown in Example 5. Note that the arrow that exits from the
rightmost box and reenters into the same box corresponds to the assembly jump
that makes the program repeat the increment of r0.
Example 6 (Progressively increasing the value contained in a register (2))
Let us consider a variation of Example 5: we want to
increase the value of register r0 from 0 to 62, and halt the program
when we reach 62. To achieve this, we cannot always jump back to the
instruction that increments r0 (as in the assembly code shown in
Example 5):
instead, we should only jump if register r0 has not yet reached the desired
value 62. Therefore, before jumping we need to compare the current value of
r0 with 62, and jump (or not) depending on the result of the comparison.
These considerations give rise to an algorithm sketched in the following flowchart (based on the flowchart in Remark 1); here, the rhombus represents a check whose result can be either true or false, and the result determines the next step.
By looking at the BlinkenBits instructions, we can see some correspondence to the rightmost part of the flowchart:
We can use the “smaller than” instruction (Table 2) to compare the value contained in
r0with the value 62 (which we must put in another register).Then, we can use a conditional jump instruction if … jump … (Table 4) to jump and repeat the increment of
r0(or not) depending on the result of the comparison.
To be converted into assembly, the flowchart is still missing some details:
the value 62 must be put into a register (e.g.,
r2) to check whether it is larger than the value inr0;the result of the comparison (which is either 0 when false, or 1 when true) must be put into a register (e.g.,
r3) to be used for the conditional jump.
With these considerations, we can refine the flowchart above as follows.
And now we can directly derive the following assembly program from the refined flowchart:
00: r0 <- 0 // Initialize r0 with value 0
01: r1 <- 1 // Initialize r1 with value 1 (to be used for increments)
02: r2 <- 62 // Maximum value we want to reach
03: r0 <- r0 + r1 // Increment r0 by 1
04: r3 <- r0 < r2 // If value in r0 is smaller than value in r2, write 1 in r3; otherwise, write 0 in r3
05: if r3 jump 3 // If r3 does _not_ contain 0 (i.e., r0 < r2 is true), jump to repeat the increment
06: halt // End of program
The key insight above is that the instruction at address 04 writes the result of
the comparison in register r3, and this result is used by the instruction at
address 05 as the condition to decide whether to jump.
As an alternative solution, we could instead check whether the value in r0 is
equal to 62, and halt the program if that is the case; if the value in r0 is
not equal to 62, we can increment r0 again. The resulting flowchart is shown
below: it is similar to the one above, but notice that the “true” and “false”
decisions to the right are swapped (because now we want to end the program when
the comparison r0 == r2 is false).
From the flowchart above we can derive the assembly program below.
00: r0 <- 0 // Initialize r0 with value 0
01: r1 <- 1 // Initialize r1 with value 1 (to be used for increments)
02: r2 <- 62 // Maximum value we want to reach
03: r0 <- r0 + r1 // Increment r0 by 1
04: r3 <- r0 == r2 // If values in r0 and r2 are equal, write 1 in r3; otherwise, write 0 in r3
05: if r3 jump 7 // If r3 does _not_ contain 0, jump to the end of the program; otherwise, continue
06: jump 3 // If we are here, then r0 is _not_ equal to r2: jump to repeat the increment
07: halt // End of program
The key insight here is that the instruction at address 06 is only executed if
the conditional jump at address 05 did not jump — and that conditional jump
is only performed if the value in r0 is equal to the value in r2.
Consequently, the instruction at address 06 is only executed if the value in
r0 is not equal to the value in r2.
Example 7 (Loading a large value into a register (2))
Let us consider again the task discussed in Example 4:
writing a program that puts the value 150 into register r0.
By looking at the other instructions in Table 3, we can observe that BlinkenBits provides an instruction that loads a value from a memory address into a register; moreover, in our assembly program we can write data 150 to describe a memory location with the desired value 150. Using these tools, we can solve the task e.g. with the following assembly program.
00: r1 <- 3 // Memory address that contains the value 150 (see below)
01: r0 <- memory@r1 // Load the value at the memory addr. pointed by r1 into r0
02: halt // End the execution here
03: data 150 // This memory location contains the value 150
Example 8 (Visualising symbols on the BlinkenBits emulator display (1))
As explained in The BlinkenBits Display, the BlinkenBits emulator has a 8-element display, where each element shows a symbol that corresponds to the content of a memory location in the range 56-63.
Our task is to write a program that shows all possible symbols on the BlinkenBits display, one symbol at a time.
To solve this task, we can modify the program in Example 5
so that, each time the program increments the value in register r0, the
program also writes the current value of r0 in the first display element. The
corresponding flowchart may look as follows.
This flowchart does not detail how the value in r0 is shown on the 1st display
element — but as seen on The BlinkenBits Display, we
need to write that value in the memory location with address 56. To achieve
this, we need to use a register-to-memory transfer instruction
(Table 3) — and that instruction, in turn,
needs to find the memory address 56 in a register, e.g., r2. Therefore, we can
refine the flowchart above as follows:
We can directly convert this refined flowchart into the following program.
00: r0 <- 0 // Initialize r0 with value 0
01: r1 <- 1 // Initialize r1 with value 1 (to be used for increments)
02: r2 <- 56 // Initialize r2 with the memory address of the display element
03: memory@r2 <- r0 // Write current value of r0 into display memory location
04: r0 <- r0 + r1 // Increment r0 by 1
05: jump 3 // Jump to perform the next increment
Tip
To better visualise how the program runs and modifies the memory contents during its execution, you can write the assembly instructions above into memory locations that are closer to the display memory: for instance, you could write the first instruction at address 48. Then, before running the program you can manually write the address 48 in the program counter (PC); alternatively, you could just initialise the PC as 0 and put a jump 48 instruction in the memory location at address 0, as follows:
00: jump 48 // Jump to the code below
48: r0 <- 0 // Initialize r0 with value 0
49: r1 <- 1 // Initialize r1 with value 1 (to be used for increments)
50: r2 <- 56 // Initialize r2 with the memory address of the display element
51: memory@r2 <- r0 // Write current value of r0 into display memory location
52: r0 <- r0 + r1 // Increment r0 by 1
53: jump 51 // Jump to perform the next increment
Example 9 (Visualising symbols on the BlinkenBits emulator display (2))
When running the program in Example 8, you may have noticed that not all values correspond to a meaningful symbol on the display. In fact, according to Table 1:
each value from 0 to 71 corresponds to a number, or letter, or mathematical operator, or punctuation symbol;
all values after 71 correspond to the symbol
👾.
Our task is to modify the program in Example 8 to stop
incrementing the displayed value at 71. To this end, before writing our code, we
can sketch the following flowchart: it is based on the one in
Example 8 with an additional check that compares the value
in r0 with 72; depending on the result of the comparison, the flowchart goes
back to display and increment the value in r0 again, or halts the program.
Before we can convert this flowchart into assembly, we need to refine the check
we just added, to make it better correspond to BlinkenBits instructions. First,
we can observe that, in order to compare the value in r0 with 72, we need to
put the value 72 into a register, e.g., into r3. Therefore, we need to add a
step to the flowchart to put the value 72 into r3, and revise the comparison
so it becomes r0 < r3. With this refinement, get this flowchart:
We cannot yet directly translate this flowchart into an assembly program
because, as we have seen in Example 6, the comparison
between r2 and r3 needs a register to save its result. However, the
flowchart above is already using all the available registers r0…r3, so we
need to reuse one of them. For instance, we can refine the flowchart above by:
using register
r3to hold the result of the comparisonr0 < r3, andif the comparison is true (i.e.,
r3contains a value that is not 0), repeat the steps from one that initialisesr3with the value 72 (since we will needr3to contain 72 to repeat the comparison).
The refined flowchart is:
We are getting very close to an assembly program, but the flowchart needs a
final refinement: for the step where we “initialise r3 with 72” we cannot
simply write the assembly instruction r3 <- 72, because 72 is outside the
allowed range 0…63. Therefore, we need to split that step into further
sub-steps, using one of two possible strategies:
as in Example 4, we could to put 72 in
r3via successive additions, oras in Example 7, we could load the value 72 from memory into
r3.
If we follow the second strategy, we can refine the flowchart as follows. Here
we write X for the address of the memory location containing the value 72;
moreover, we use register r3 to initially contain the address X, and we
immediately reuse r3 to hold the value read from memory address X (i.e., the
value 72).
We can now directly translate this flowchart into the assembly program below. Note that here we put the value 72 into the memory location at address 10 (but we could have used any other address).
00: r0 <- 0 // Initialize r0 with value 0
01: r1 <- 1 // Initialize r1 with value 1 (to be used for increments)
02: r2 <- 56 // Memory address of the display element
03: r3 <- 10 // Memory addr. with the max value to display (see below)
04: r3 <- memory@r3 // Load from memory the maximum value we wish to display
05: memory@r2 <- r0 // Write current value of r0 into display memory location
06: r0 <- r0 + r1 // Increment r0 by 1
07: r3 <- r0 < r3 // If value in r0 is smaller than value in r2, write 1 in r3; otherwise, write 0 in r3
08: if r3 jump 3 // If r3 does _not_ contain 0, jump to repeat the increment
09: halt // End of program
10: data 72 // This memory location contains the max value to display
You can observe that this program uses the register r2 at different times for
different purposes:
the instruction at address 02 uses
r2to hold the memory address 10;the instruction at address 03 loads the value contained at the memory location with address 10 (i.e., the value 71) and writes it into register
r2: from this point on, the program usesr2to hold the maximum value to display.
The program also uses register r3 at different times for different purposes:
the instructions at addresses 04 and 05 use register
r3to hold the memory address of the display element;then, the comparison at address 07 overwrites the content of register
r3, and the result of the comparison is used for the conditional jump at address 08. For this reason, the conditional jump goes back to the instruction at address 04, which restores the correct display memory address inr3.
Example 10 (Summing multiple values stored in memory (1))
Our task is to write a program that computes the sum of values contained in memory locations with consecutive addresses. The requirements for the program are the following:
When the program starts, register
r0contains the address of the first value to sum;When the program ends, register
r1must contain the result of the sum. The content of the other registers is not important.The program must sum all values it finds in memory starting with the one at the memory location whose address is in register
r0; the program keeps reading and summing the values stored at consecutive memory locations, until it reaches a memory location that contains the value 0.
To solve this task, we can:
use register
r1as an accumulator that contains the current result of the summation, starting with 0;use register
r2to hold the next value to be added to the summation (that value is loaded from the memory address in registerr0); andafter each addition, increment the value contained in
r0by 1, thus making it point to the memory location of the next value to add.
Importantly, after step 2, we need to check whether the value loaded from memory
is 0 — and if so, we must halt the program. These ideas lead us to this
flowchart:
To translate this flowchart into assembly, we need to further refine some of its steps, similarly to what we did in the previous examples. Specifically, these steps should be refined into several sub-steps (and correspondingly, into several assembly instructions):
The comparison that checks whether the value in
r2is equal to 0;The increment of the value in
r0by 1.
After such refinements (try to apply them yourself!), we can derive an assembly program like the one below.
Note
In the following assembly program, the values to be used for the
summation are at the memory addresses 10…13. Therefore, the program should be
executed by first manually setting register r0 to 10. When the program halts,
the register r1 will contain the summation result 42, as required.
00: r1 <- 0 // Current result of the summation
01: r2 <- memory@r0 // Load from memory the next value to add
02: r3 <- 0 // Value 0 used for the comparison below
03: r3 <- r3 == r2 // Is the last-loaded value (in r2) equal to zero?
04: if r3 jump 09 // If the last-loaded value is zero, jump to end of program
05: r1 <- r1 + r2 // Increment the summation result with the last-loaded value
06: r3 <- 1 // Value 1 to be used for incrementing r0
07: r0 <- r0 + r3 // Increment r0, so it points to the next value to add
08: jump 1 // Jump to perform the addition of the next value
09: halt
10: data 12 // Value to be added
11: data 2 // Value to be added
12: data 7 // Value to be added
13: data 21 // Value to be added
14: data 0 // End of the values to be added
15: data 33 // This value will not be added: the sum will stop earlier
You can observe that the register r3 is used at different times for different
purposes:
the instructions at addresses 02 and 03 use
r3to hold the value 0 (for comparing with the value loaded from memory), andthe instructions at addresses 06 and 07 use
r3to hold the value 1 (for incrementing the address inr0).
Example 11 (Summing multiple values stored in memory (2))
This is a variation of Example 10: the task is now to compute the summation of \(n\) values contained in memory locations with consecutive addresses. The requirements for the program are the following:
when the program starts, register
r0contains the address of the first value to sum, and registerr3contains the number of values to sum;when the program ends, register
r1must contain the result of the sum. The content of the other registers is not important.
To solve this task, we can adapt the approach of Example 10:
use register
r1as an accumulator that contains the current result of the summation, starting with 0;use register
r2to hold the next value to be added to the summation (that value is loaded from the memory address in registerr0); andafter each addition, increment the value contained in
r0by 1, thus making it point to the memory location of the next value to add;moreover, we now need to count how many values we have added. According to the task description, the number of values to add is initially given in register
r3: so, we can decrement the value contained inr3after each addition, and halt the program when that value becomes 0.
Here is a flowchart that summarises these ideas:
After refining this flowchart (try it yourself!), we can derive an assembly
program like the one below. Compared to the the assembly program of
Example 10, the program below uses register r2
for various purposes, whereas register r3 always contains the number of values
that are left to be added.
Note
In the following assembly program, the values to be used for the
summation are at the memory addresses 11…16. Therefore, the program should be
executed by first manually setting register r0 to 11, and register r3 to 6.
When the program halts, the register r1 will contain the summation result 75.
00: r1 <- 0 // Current result of the summation
01: r2 <- 0 // Value 0 used for the comparison below
02: r2 <- r3 == r2 // Do we have 0 values left to add?
03: if r2 jump 10 // If yes, we are done: jump to the end of the program
04: r2 <- memory@r0 // Load from memory the next value to add
05: r1 <- r1 + r2 // Increment the summation result with the last-loaded value
06: r2 <- 1 // Value 1 for incrementing r0 and decrementing r3
07: r0 <- r0 + r2 // Increment r0, so it points to the next value to add
08: r3 <- r3 - r2 // Decrement r3, to remember we have one less value to add
09: jump 1 // Jump to perform the addition of the next value
10: halt
11: data 12 // Value to be added
12: data 2 // Value to be added
13: data 7 // Value to be added
14: data 21 // Value to be added
15: data 0 // Value to be added
16: data 33 // Value to be added
References and Further Readings#
You are encouraged to read the following sections of the reference book:
Section 1.1 - “Computer Processing”
Section 1.2 - “Hardware Components”
The following appendix of the reference book may be also useful:
Appendix B - “Number Systems” (in particular, binary)
Lab: Programming Exercises with BlinkenBits#
Note
The exercises above (from Exercise 1 to Exercise 5) and the ones below are not part of the course assessment: their purpose is to let you experiment with programming, in a limited setting where you only have a few tools (i.e., BlinkenBits assembly instructions) to use. The difficulty of the exercises increases progressively, and the last ones are quite tricky. Here are some recommendations.
Try solving all the exercises you can; feel free to try them again later during the course.
Before writing assembly code, it may be helpful to sketch your algorithm as a flowchart, and then refine the flowchart, until you can derive assembly code from it (as we did in the examples above).
Compare your solutions with those written by your fellow students, and then with the solutions
Ask for feedback to the teacher and TAs.
Feel free to experiment by writing your own BlinkenBit programs — e.g., programs that show some interesting animation on the BlinkenBits display. You are welcome to post your creations on the discussion forum on DTU Learn (but please do not post your solutions to the exercises below).
Exercise 6 (Loading a large value into a register (1))
Consider the BlinkenBits assembly code given as a solution to the task in
Example 4: it is using all 4 registers r0…r3 to achieve
the final goal of having register r0 contain the value 150. Try to change the
solution to make it use less registers.
Hint
Consider that, as shown in the last instruction in Example 4, the same register can be used both as operand of the addition, and as the target where the result of the addition will be written…
Exercise 7 (Loading a large value into a register (2))
This is a follow-up to Example 4 and/or
Exercise 6: write a BlinkenBits assembly program that puts
the value 2024 into register r0. Write two versions of the program:
Exercise 8 (Swapping values (1))
Write a program that swaps the values contained in registers r0 and r1.
The program should work as follows:
before running the program, you should write any values you like in the registers
r0andr1;after the program runs and halts, register
r1must contain the value that was initially contained inr0— and vice versa, registerr0must contain the value that was initially contained inr1.
The content of the other registers is not important and you can change it freely.
For instance, if you set r0 to 42 and r1 to 430, and then run the program,
then the program must run and halt by leaving r0 set to 430 and r1 set to
42.
Hint
You can use another register (besides r0 and r1) to temporarily hold the
one of the values that is being swapped…
Exercise 9 (Swapping values (2))
Write a program that swaps the values contained in the memory locations contained in the memory locations 19 and 20.
The program should work as follows:
before running the program, you should set all registers to 0 and write any values you like in the memory locations with addresses 19 and 20;
after the program runs and halts, memory location 19 must contain the value that was initially contained in the memory location 20 — and vice versa, memory location 20 must contain the value that was initially contained in the memory location 19.
The content of the registers is not important and you can change it freely.
Hint
Your program will need to put the memory addresses 19 and 20 into some registers, in order to read/write the memory contents using the BlinkenBits register-memory transfer instructions (Table 3).
To swap the values, you can build upon your solution to Exercise 8.
Exercise 10 (Blinking asterisk)
Your task is to write a program that shows a blinking asterisk on the first
element of the BlinkenBits display. The blinking should be obtained by
alternating the symbols _ and *.
Hint
To solve this task, you can write a program that uses a jump to repeat the displaying of the desired symbols, over and over.
From The BlinkenBits Display we know that:
the first element of the display visualises the value contained in the memory location with address 56;
moreover, the symbols
_or*are visualised when that memory location contains the values 62 or 70, respectively.
Exercise 11 (Multiplication)
Your task is to write an assembly program that multiplies the value contained in
register r0 by the value contained in r1, writes the result in r0, and
halts. When the program halts, the content of the other registers besides r0
is not important.
Hint
Remember that multiplying \(m\) by \(n\) is equivalent to computing \(n\) additions \(m + m + m + ...\). To this purpose, you may use a register to accumulate the results of the ongoing additions; after the last addition, that register will contain the result of the multiplication.
You will need to count how many additions you have performed. To this purpose, your program might:
decrease the value in
r1by 1 every time it performs an addition, until the value inr1becomes 0;if the value in
r1is 0, the multiplication is complete.
Exercise 12 (Division)
Your task is to write an assembly program that divides the value contained in
register r0 by the value contained in r1 (which you can assume different
from 0), writes the result in r0, and halts. When the program halts, the
content of the other registers besides r0 is not important.
Hint
You can follow a strategy similar to Exercise 11, except that dividing \(m\) by \(n\) is equivalent to counting how many subtractions \(m - n - n - n - ...\) you can perform, before reaching a value that is smaller than the divisor \(n\).
Exercise 13 (Division and remainder)
This is a small variation of Exercise 12. Your task is to write an
assembly program that divides the value contained in register r0 by the value
contained in r1 (which you can assume different from 0), writes the division
result in r0 and the division remainder in r1, and then halts. When the
program halts, the content of the other registers besides r0 and r1 is not
important.
Hint
Your solution to Exercise 12 should be already computing the remainder of the division. So, you may just need to make sure that the the reminder is copied into
r1before the program halts…
Exercise 14 (Displaying a 2-digit decimal number)
Write a program that shows the value contained in register r0 on the
BlinkenBits display, as a decimal number, and then halts. You can assume that
the value contained in r0 is between 0 and 99.
For instance, if r0 contains the value 42, then the program should display the
digits 4 and 2, as follows:

Hint
The solution to this exercise is can be based on
Exercise 13: if you divide the value in r0 by 10, then
the result of the division is the number of tens, and the remainder of the
division is the number of units. You just need to show such numbers on the
BlinkenBits display…
Exercise 15 (Complex expression)
Write a program that reads computes the result of the expression
((a + b) * (c - d)) / e, where the values of a, b, c, d, and e
are contained in some memory locations of your choice. The program
must write the result of the computation into register r0, and then halt.
The content of the other registers is not important.
Hint
Your program will need to compute the result of each sub-expression, storing its result into some register, so that result can be used for further computations. More concretely:
in order to compute the whole expression, you will need to first compute the result of the sub-expression ((a + b) * (c - d)) and put it into a register;
in order to compute the result of this sub-expression, you will need to compute the result of both its sub-expressions (a + b) and (c - d) and put their results into registers;
in order to compute the result of (a + b), you will need to load the values of a and b from memory into registers;
similarly, in order to compute the result of (c - d), you will need to load the values of c and d from memory into registers.
Your solution for this exercise should build upon the solutions to Exercise 11 and Exercise 12.
Exercise 16 (Moving “1”)
Your task is to write a program that displays 0 in all display elements, and
an animated 1 that changes position moving from the left to the right of the
display. When the 1 reaches the rightmost element of the display, it goes back
to the first element.
The resulting animation should look as follows (but feel free to experiment and make it look slightly different):

Hint
To solve this task, you may take some inspiration from your solution to Exercise 10.
First, you may write a program that shows
1and then0on the first display element.Then, you may consider what it takes to make that program display
1and then0on a display element with a different memory address:you may e.g. duplicate your code, but using a different display memory address to show
1and then0at a different position;or, you may let your program change the address of the display element where
1and0are being shown:that address is a value contained in a register, and if you increment that value by one, you get the address of the next display element;
after you increment the display element memory address, you may use a jump to execute again the code that displays
1and0;if you follow this idea, then your program will need to check whether it has reached the address of the last display element (at address 63) — and if so, the program must not increment the address further. Instead, the program must change the address to use the first display element again…
Exercise 17 (Moving alien)
Your task is to write a program that displays an alien symbol 👾 that moves left-to-right
and right-to-left on the BlinkenBits display, as follows:

Hint
Remember that, according to Table 1, the alien symbol
👾is shown if a display memory location contains a value in the range 72…4095.It may be helpful to use the solution to Exercise 16 as a starting point.
It can be helpful to split the program in two parts: one that moves the alien left-to-right, and another that moves the alien right-to-left. You can use a conditional jump to execute one part of the program or the other, depending on whether the alien has reached the leftmost or rightmost position of the display.
Exercise 18 (Hard: sorting numbers on the BlinkenBits display)
Write a program that sorts the values displayed on the BlinkenBits display.
For instance: if the BlinkenBits display is visualising the digits
8 3 9 3 7 6 1 5 when the program starts, then it should visualise the digits
1 3 3 5 6 7 8 9 when the program halts.
Hint
It may help to start writing a program that simply swaps the content of the 1st display element with lowest value contained in the remaining display elements. To this purpose, you might build upon your solution to Exercise 9.
Then, you could improve this program by repeating the swap, targeting the 2nd display element, then the 3rd, then the 4th…
Solutions to the Exercises#
Solution to Exercise 6#
Here is a possible solution using only two registers (r0 and r1):
00: r0 <- 63 // Write value 63 into register r1
01: r1 <- 24 // Write value 24 into register r2
02: r0 <- r0 + r0 // Add value contained in r0 to itself, write result in r0
03: r0 <- r0 + r1 // Add values contained in r0 and r1, write result in r0
04: halt
Solution to Exercise 7
Here is a possible solution, adapted from the solution above.
00: r0 <- 63 // Write value 63 into register r1
01: r1 <- 8 // Write value 24 into register r2
02: r0 <- r0 + r0 // Add value contained in r0 to itself, write result in r0
03: r0 <- r0 + r0 // Add value contained in r0 to itself, write result in r0
04: r0 <- r0 + r0 // Add value contained in r0 to itself, write result in r0
05: r0 <- r0 + r0 // Add value contained in r0 to itself, write result in r0
06: r0 <- r0 + r0 // Add value contained in r0 to itself, write result in r0
07: r0 <- r0 + r1 // Add values contained in r0 and r1, write result in r0
08: halt
Solution to Exercise 8
00: r2 <- r1 // Remember the value contained in r1 before the swap
01: r1 <- r0 // Copy the value contained in r0 into r1
02: r0 <- r2 // Copy the value contained in r2 (which was in r1) into r0
03: halt
Solution to Exercise 9
00: r2 <- 19 // Memory address of the first value to swap
01: r3 <- 20 // Memory address of the second value to swap
02: r0 <- memory@r2 // Load first value from memory into r0
03: r1 <- memory@r3 // Load second value from memory into r1
04: memory@r3 <- r0 // Store value contained in r0 into 2nd memory address
05: memory@r2 <- r1 // Store value contained in r1 into 1st memory address
06: halt
Solution to Exercise 10
00: r0 <- 56 // Address of the first display element
01: r1 <- 8 // Memory address containing the value for '_' (see below)
02: r1 <- memory@r1 // Load value of underscore symbol '_' from memory
03: r2 <- 9 // Memory address containing the value for '*' (see below)
04: r2 <- memory@r2 // Load value of asterisk symbol '*' from memory
05: memory@r0 <- r1 // Show an underscore on the first display element
06: memory@r0 <- r2 // Show an asterisk on the first display element
07: jump 5 // Jump back to repeat the blinking
08: data 62 // Value displayed as the underscore symbol '_'
09: data 70 // Value displayed as the asterisk symbol '*'
Solution to Exercise 11
00: r2 <- 0 // Write the temporary result into r2 (initially 0)
01: r3 <- 0 // Write value 0 into r3
02: r3 <- r1 == r3 // Is the value in r1 equal to 0?
03: if r3 jump 8 // If so, multiplication is complete: jump to end of the program
04: r2 <- r2 + r0 // Add the value in r1 to the temporary result in r2
05: r3 <- 1 // Write the value 1 into r3
06: r1 <- r1 - r3 // Decrement the operand in r0 by 1
07: jump 1 // Jump to repeat the code above
08: r0 <- r2 // Move the final result of the multiplication into r0
09: halt
Solution to both Exercise 12 and Exercise 13
00: r2 <- 0 // Write the temporary result into r2 (initially 0)
01: r3 <- r0 < r1 // Check if the dividend (r0) is smaller than the divisor (r1)
02: if r3 jump 7 // If so, the division is complete: jump to end of the program
03: r0 <- r0 - r1 // Subtract the divisor from the dividend
04: r3 <- 1 // Write value 1 into r3
05: r2 <- r2 + r3 // Add 1 to the temporary result in r2
06: jump 1 // Jump to repeat the code above
07: r1 <- r0 // r0 contains the remainder: copy it into r1
08: r0 <- r2 // Copy the final result of the division from r2 into r0
09: halt
Solution to Exercise 14
00: r2 <- 0 // Write the temporary division result into r2 (initially 0)
01: r1 <- 10 // Write divisor (10) into r1
02: r3 <- r0 < r1 // Check if the dividend (r0) is smaller than the divisor (r1)
03: if r3 jump 8 // If so, the division is complete: jump below to display result
04: r0 <- r0 - r1 // Subtract the divisor from the dividend
05: r3 <- 1 // Write value 1 into r3
06: r2 <- r2 + r3 // Add 1 to the temporary result in r2
07: jump 2 // Jump to repeat the code above
08: r3 <- 62 // Put memory address of the second-to-last display element into r3
09: memory@r3 <- r2 // Show the division result (i.e., number of tens) on the display
10: r3 <- 63 // Put memory address of the last display element into r3
11: memory@r3 <- r0 // Show the division remainder (i.e., number of units) on the display
12: halt
Solution to Exercise 15
The solution below reads the values of \(a\), \(b\), \(c\), \(d\), and \(e\) from the memory locations at addresses 30–34. If you change those values, the code below will compute a different result.
00: r0 <- 30 // Address of 'a'
01: r0 <- memory@r0 // Load 'a' into r0
02: r1 <- 31 // Address of 'b'
03: r1 <- memory@r1 // Load 'b' into r1
04: r0 <- r0 + r1 // Add 'a' and 'b', storing the result in r0
05: r2 <- 32 // Address of 'c'
06: r2 <- memory@r2 // Load 'c' into r2
07: r3 <- 33 // Address of 'd'
08: r3 <- memory@r3 // Load 'd' into r3
09: r1 <- r2 - r3 // Subtract 'd' from 'c', storing the result in r1
10: r2 <- 0 // Write the temporary multiplication result into r2 (initially 0)
11: r3 <- 0 // Write value 0 into r3
12: r3 <- r0 == r3 // Is r0 equal to 0?
13: if r3 jump 18 // If so, the multiplication is complete: jump to the division code
14: r2 <- r2 + r1 // Add the operand in r1 to the temporary result in r2
15: r3 <- 1 // Write value 1 into r3
16: r0 <- r0 - r3 // Decrement the operand in r0 by 1
17: jump 11 // Jump to the beginning of the multiplication code
18: r0 <- r2 // Move the final result of multiplication into r0
19: r1 <- 34 // Address of 'e'
20: r1 <- memory@r1 // Load 'e' into r1
21: r2 <- 0 // Write the temporary division result into r2 (initially 0)
22: r3 <- r0 < r1 // Check if the dividend (r0) is smaller than the divisor (r1)
23: if r3 jump 28 // If so, the division is complete: jump after the division code
24: r0 <- r0 - r1 // Subtract the divisor from the dividend
25: r3 <- 1 // Write value 1 into r3
26: r2 <- r2 + r3 // Add 1 to the temporary result in r2
27: jump 22 // Jump to the beginning of the division code
28: r0 <- r2 // Move the final result of division (and the entire computation) into r0
29: halt
30: data 8 // Value of a
31: data 17 // Value of b
32: data 55 // Value of c
33: data 23 // Value of d
34: data 20 // Value of e
Solution to Exercise 16
00: r0 <- 0 // Value for later use
01: r1 <- 1 // Value for later use
02: r2 <- 56 // Init target position of '1' in display memory
03: r3 <- 63 // Max address to reach in display memory
04: memory@r2 <- r1 // Write '1' in the target display memory position
05: memory@r2 <- r0 // Write '0' in the target position
06: r3 <- r2 == r3 // Has r2 reached the display memory max address?
07: if r3 jump 2 // Jump if previous check was true
08: r2 <- r2 + r1 // Increment target display position
09: jump 3 // Jump to the beginning of the program
Solution to Exercise 17
00: r0 <- 56 // Current position of alien in r0 (initially 56, address of 1st display element)
01: r2 <- 63 // Write the memory address of the last display element into r2
02: r2 <- r0 == r2 // Check if we have reached the last position of the display
03: if r2 jump 13 // If so, jump to the move-backwards part of the code
04: r2 <- 0 // Value '0' to be displayed
05: r3 <- 26 // Write mem address of the value corresponding to the '👾' symbol into r3
06: r3 <- memory@r3 // Load the '👾' symbol into r3
07: r1 <- 1 // Write 1 into r1 (to be used for the increment below)
08: r1 <- r0 + r1 // Write the new position (r0 + 1) into r1
09: memory@r0 <- r2 // Display a '0' at the current position
10: memory@r1 <- r3 // Display the alien at the new position
11: r0 <- r1 // Update the current position with the new position
12: jump 1 // Jump to the start of the move-forwards part of the code
13: r2 <- 56 // Write the memory address of the first position of the display (56) into r2
14: r2 <- r0 == r2 // Check if we have reached the first position of the display
15: if r2 jump 1 // If so, jump to the move-forwards part of the code
16: r2 <- 0 // Value '0' to be displayed
17: r3 <- 26 // Write mem address of the value corresponding to the '👾' symbol into r3
18: r3 <- memory@r3 // Load the '👾' symbol into r3
19: r1 <- 1 // Write 1 into r1 (to be used for the decrement below)
20: r1 <- r0 - r1 // Write the new position (r0 - 1) into r1
21: memory@r0 <- r2 // Display a '0' at the current position
22: memory@r1 <- r3 // Display the alien at the new position
23: r0 <- r1 // Update the current position with the new position
24: jump 13 // Jump to the start of the move-backwards part of the code
25: halt
26: data 72 // Value of the '👾' symbol
56: data 72 // First display cell, with the alien (will be changed by the program)
Solution to Exercise 18
The last lines of the program contain the initial values of the BlinkenBits display elements, which will be modified and sorted while the program runs. You can change them to see the program sorting a different sequence of values.
00: r0 <- 56 // Write address of 1st number to be checked into r0 (initially 56)
01: r1 <- 63 // Write address of the last display element into r1
02: r1 <- r0 == r1 // Check if the position of 1st number is the same as the last display element
03: if r1 jump 22 // If so, we are done, jump to the end of the program
04: r1 <- 1 // Write 1 into r1 (for the increment below)
05: r1 <- r0 + r1 // Write the position of the 2nd number to be checked into r1 (initially the one right after the first number)
06: r2 <- 63 // Write the position of the last display element into r2
07: r2 <- r2 == r1 // Check if the position of the 2nd number is the last display element
08: if r2 jump 19 // If so, the current sorting is complete: jump to move to the next value
09: r2 <- memory@r0 // Load the first number into r2
10: r3 <- memory@r1 // Load the second number into r3
11: r2 <- r2 < r3 // Check if the first number is smaller than the second number
12: if r2 jump 16 // If so, no need to swap: jump to compare against the next value
13: r2 <- memory@r0 // Load the first number into r2
14: memory@r1 <- r2 // Store the first number at the position of the second number
15: memory@r0 <- r3 // Store the second number at the position of the first number
16: r2 <- 1 // Write 1 into r2 (for the increment below)
17: r1 <- r1 + r2 // Update the position of the second number to be checked (i.e. go to the next number)
18: jump 6 // Jump above to compare the two currently-selected numbers
19: r1 <- 1 // Write 1 into r2 (for the increment below)
20: r0 <- r0 + r1 // Update the position of the first number to be checked (i.e. go to the next number)
21: jump 1 // Jump to compare the current 1st number with the ones that follow
22: halt
56: data 8 // Initial content of 1st display element
57: data 3 // Initial content of 2nd display element
58: data 9 // Initial content of 3rd display element
59: data 3 // Initial content of 4th display element
60: data 7 // Initial content of 5th display element
61: data 6 // Initial content of 6th display element
62: data 1 // Initial content of 7th display element
63: data 5 // Initial content of 8th display element
